MURATA Makoto (FAMILY Given)
Fuji Xerox Information Systems
This note shows preliminaries of the hedge automaton theory. In the XML community, this theory has been recently recognized as a simple but powerful model for XML schemata. In particular, the design of RELAX (REgular LAnguage for XML) is directly based on this theory.
First, we introduce hedges. Informally, a hedge is a sequence of trees. In the XML terminology, a hedge is a sequence of elements possibly interevened by character data (or types of character data); in particular, an XML document is a hedge.
A hedge over a finite set Σ (of symbols) and a finite set X (of variables) is:
Figure 1 depicts three hedges: a <ε> , a <x > , and a <ε > b < b <ε> x > . Observe that elements of Σ (i.e., a and b ) are used as labels of non-leaf nodes, while elements of X (i.e., x ) are used as labels of leaf nodes. We abbreviate a <ε> as a. Thus, the third example is denoted by a b <b x > .

Figure 1. Three hedges: a <ε> , a <x > , and a <ε > b < b <ε> x >
Next, we consider an XML document. Suppose that Σ = {doc, title, image, para} and X ={#PCDATA}. Then, doc < title<#PCDATA> para<#PCDATA> <image/> para<#PCDATA>> is a hedge. In the XML syntax, this hedge can be represented as below:
<doc>
<title>#PCDATA</title>
<para>#PCDATA</para>
<image/>
<para>#PCDATA</para>
</doc>
In this section, we introduce regular hedge grammars (RHGs). An RHG is a mechanism for generating hedges. In other words, an RHG describes a set of hedges.
Since the primary role of an XML schema is to describe a set of valid documents, an RHG can be considered as a formal representation of a XML schema.
A regular hedge grammar (RHG) is a 5-tuple <Σ, X, N, P,rf >, where:
Now, we consider derivaton of RHGs. Informally speaking, given a sequence of non-terminals, we repeatedly replace non-terminals with hedges in the right-hand side of corresponding production rules.
Hedge v is directly derived from hedge u when:
The language generated by G, denoted by L(G), is the set of hedges which are derived from some non-terminal sequence that matches rf .
Consider an RHG G = < a, x, {n1 , n2}, P, n1?>, where:
P = {n1 → a<n2+ >, n2 → x }.
Then,
L(G) ={ε, a<x >, a<xx>, a<xxx >, ...}
Next, we construct an RHG that mimicks a DTD. As an example, consider a DTD as follows:
<!ELEMENT doc (title, (para|image)*)> <!ELEMENT title (#PCDATA)> <!ELEMENT para (#PCDATA)> <!ELEMENT image EMPTY>
This DTD can be captured by an RHG G = <Σ, X, N, P, nd > where
Next, consider an RHG G = <Σ, X, N, P, n1 > where:
Both the rule for non-terminal n1 and that for n2 have segment in the right-hand side. However, the former has content model np* n2*, and the latter has content model np*. This impiles that top-level segments can have subordinate segments, but these subordinate segments cannot have subordinate segments.
The DTD syntax cannot exactly capture this RHG, since every occurrence of segments is forced to have the same content model. The smallest DTD that covers this RHG is as below:
<!ELEMENT segment (para*, segment*)> <!ELEMENT para (#PCDATA)>
Observe that this DTD allows unlimited nesting of segments. Since the DTD syntax does not allow two content models for segments, this DTD uses one loose content model.
In this section, we introduce deterministic hedge automata and non-deterministic hedge automata.
A deterministic hedge automaton (DHA) is < Σ, X, Q, α, ι, F>, where:
Figure 2 shows the execution of a DHA for a hedge shown in Figure 1.
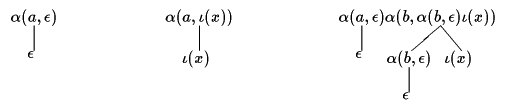
Figure 2.Execution of a deterministic hedge automaton
Next, we show a DHA that accepts the first example in Section 2. Let M = <a , x , { q0, q1, q2 }, α, ι, q1? }, where:
Then,
L(G) ={ε , a<x> , a<xx> , a<xxx> , ... }
Next, we introduce non-deterministic hedge automata. A non-deterministic hedge automaton (NDHA) is < Σ, X, Q, α, ι, F>, where:
By definition, a DHA is also a NDHA. We only have to confuse a state and a singleton set containing that state. Thus, the above DHA is also an example of NDHAs.
The last example RHG in Section \ref{RHG} can be readily captured by a NDHA <Σ, X, Q, α, ι, F >, where
The following conditions are equivalent.
The proof that (3) implies (2) is done by the subset construction. The rest of the proof is straightforward.
Suppose that set L1 and L2 are accepted by (N)DHA M1 and M2, respectively. We can effectively construct (N)DHAs that accept the following languages.
The set of parse trees of an extended context-free grammar is said to be a local tree language. A lot is known about the relationships between local tree languages and regular hedge languages. We mention two observations which are directly relevant to XML.
Observation (1) implies that RHGs are more powerful than DTDs, while (2) ensures that given any RHG, we can construct a reasonable DTD.
In the theoretical computer science community, regular hedge languages were first studied by Pair et al[PQ68] and Takahashi[Tak75]. Regular hedge language can also be considered as extensions of regular tree languages [Tha67]. We borrow some concepts from these papers but adopt definitions more similar to those for regular string languages.
We define RHG's similarily to [PQ68,Tak75], but we avoid projections. Alternatively, our definition can be considered as a hedge-version of Brainerd's tree regular grammars (called "tree generating regular systems) [Bra69].
Our definitions of NDHAs and DHAs are derived from (non-)deterministic tree automata of [Tha67] except that we have extended them to hedges.
It was Kil-Ho Shin (Fuji Xerox) who first proposed to use regular hedge languages as a formal model for schemata of structured documents. His proposal dates back to November, 1991, but he never published any papers. In search of a formalism for document schemata, HIYAMA Masayuki (FAMILY Given) reached a similar formalism in 1996. Since 1993, the present author has applied regular hedge languages (and hedge monoids, which are outside the scope of this note) for schema transformation [Mur97a,Mur97b,Mur98].
The word ``hedge'' was originally proposed by Bruno Courcelle [Cou89]. Derick Wood recommended the use of this word, and it has become the standard word in the XML community after a tutorial by Paul Prescod in 1999. For more information, see the special section on hedge automata in the he SGML/XML Web Page (http://www.oasis-open.org/cover/topics.html#forestAutomata).
[Mur97a] Makoto Murata. DTD transformation by patterns and contextual conditions. In Proceedings of SGML/XML'97 (Also available at http://www.fxis.co.jp/DMS/sgml/xml/sgmlxml97.html and http://www.fxis.co.jp/DMS/sgml/xml/dtd_transformation/index.html) . GCA, 1997.
[Tha87] James W. Thatcher. Tree automata: An informal survey. In Alfred V. Aho, editor, Currents in the theory of computing, pages 143--172. Prentice-Hall, 1987.